Dentro de los modelos que manejo, tengo el siguiente que voy a empezar en un mes a probar en tiempo real gracias al Broker De Giro, si las comisiones que cobran son 3 euros por operación los números salen.
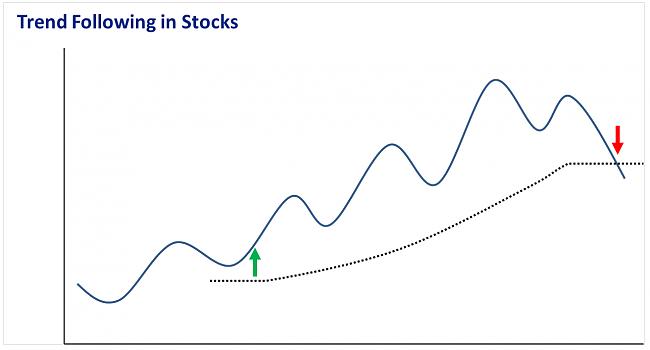
Se trata de un sistema de búsqueda de tendencias en ETFs del
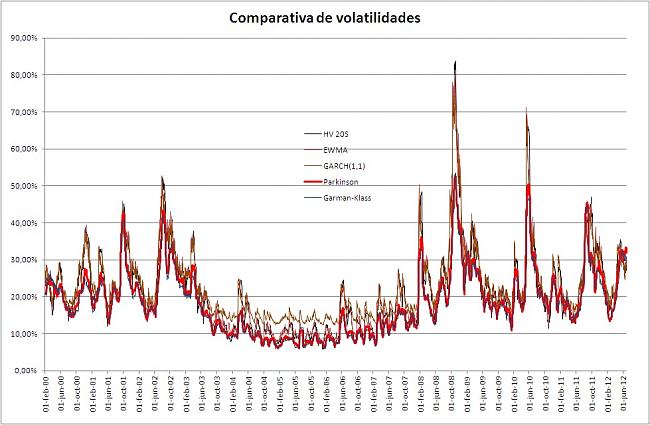
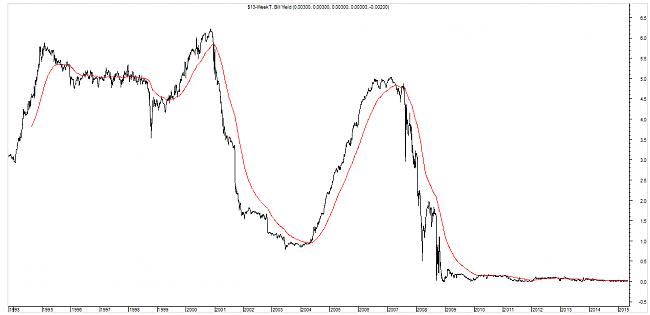
VIX
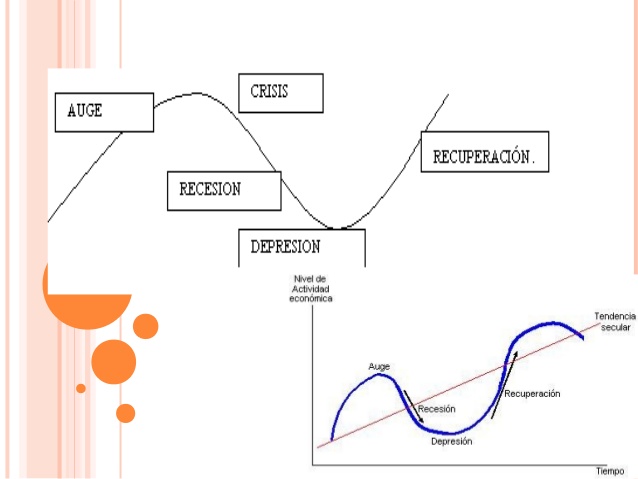
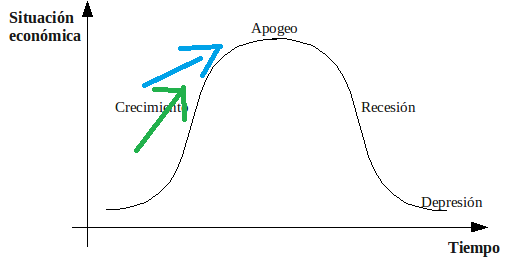
El VIX es un índice de volatilidad del S&P500
The CBOE Volatility Index® (VIX® Index®) is a key measure of market expectations of near-term volatility conveyed by S&P 500 stock index option prices. Since its introduction in 1993, the VIX Index has been considered by many to be the world's premier barometer of investor sentiment and market volatility. Several investors expressed interest in trading instruments related to the market's expectation of future volatility, and so VX futures were introduced in 2004, and VIX options were introduced in 2006.
Options and futures on volatility indexes are available for investors who wish to explore the use of instruments that might have the potential to diversify portfolios in times of market stress.
Please visit the links on this page to explore how you could use VIX-related products in the management of your investment portfolio.
Tiene mucho riesgo, de hecho han habido días que ha variado cerca del 45%
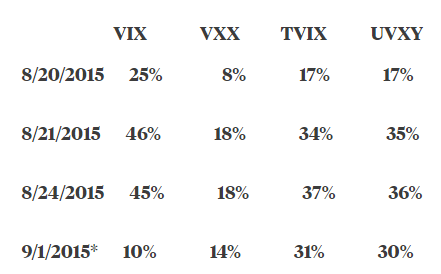
Es necesario controlar el riego, pero estás altas volatilidades son buenas porque permite según el
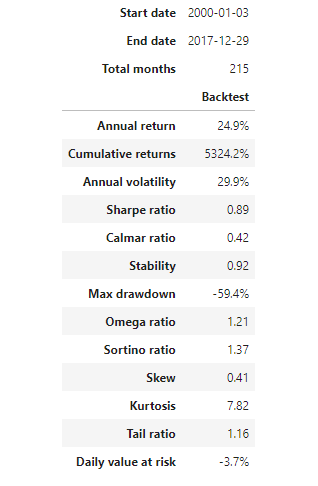
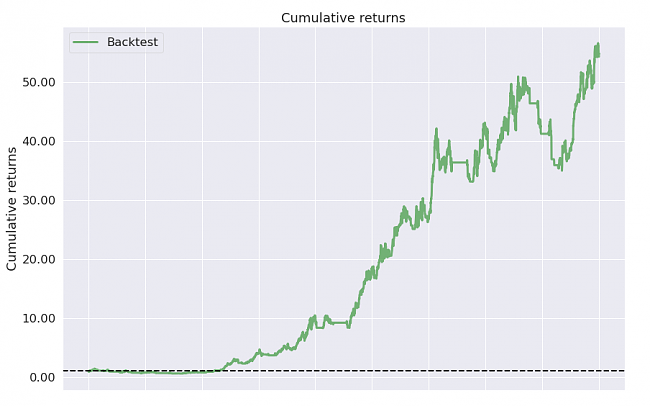
sistema multiplicar el dinero por 13 en 6 años, por lo tanto es un sistema de mucho riesgo, por eso hay que invertir poco dinero por ejemplo 1000 euros y ver que pasa.
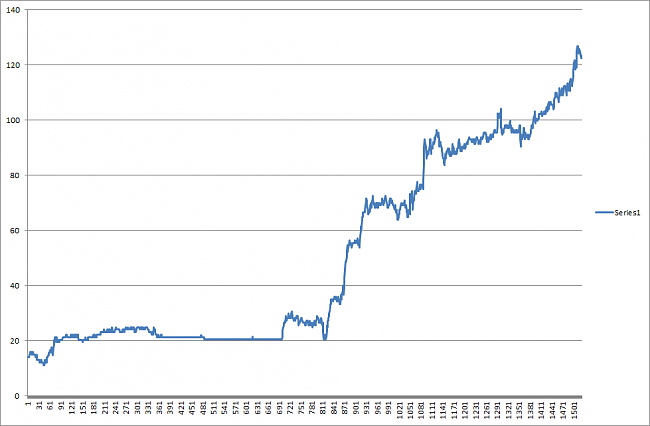
Más que este caso extremo, que es demasiado bonito para ser verdad. La idea final es tener unos cuantos sistemas que operen simultáneamente buscando activos en tendencias. Lo ideal es operar con índices porque
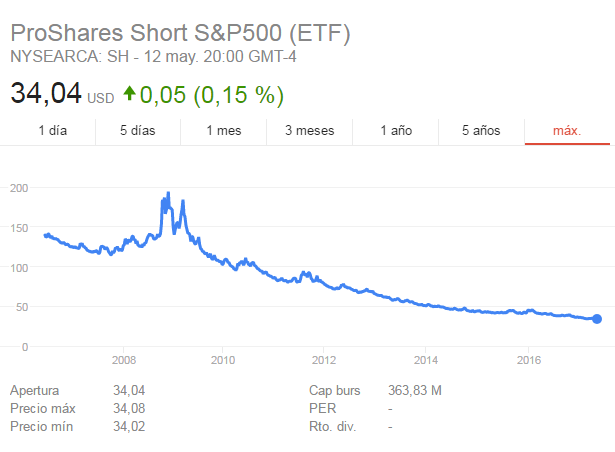
permite ponerse corto y así aprovechar cuando un índice entra en una fuerte corrección.
El problema de estos sistemas es que no eran rentables para un inversor particular, por las elevadas comisiones de los brokers, no puede ser que te cobraran 25 o más euros por cada operación, si las cifras de DE GIRO son ciertas, estos sistemas
pueden ser muy rentables.
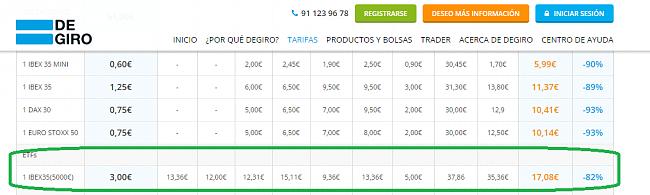
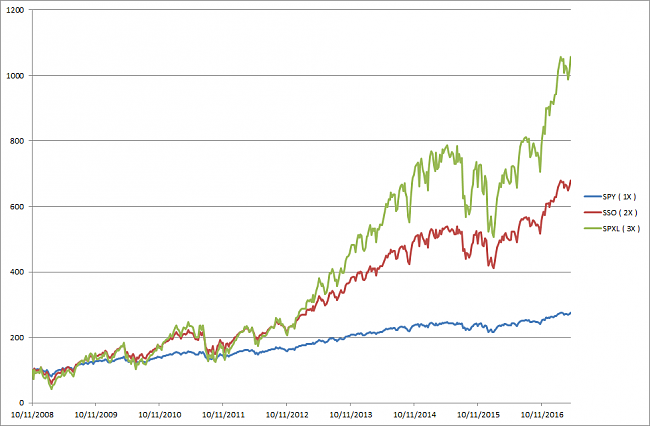
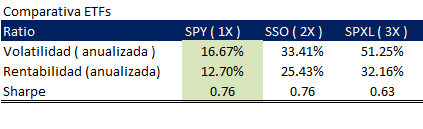
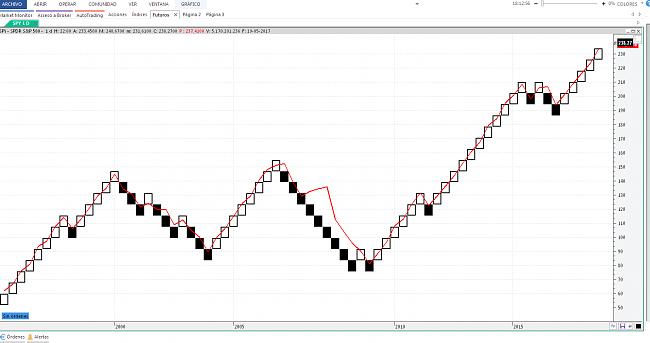
Se trata de operar en una cartera de ETFs que te puedas poner corto, con apalancamientos 1X, al final se trata de hacer un backtesting, para ver como se comportaría el sistema.
Los
CFDs son un timo, nunca vas a ganar dinero, es una trampa legal que los brokers se inventan para engañar a los inversores minoristas. En Estados Unidos están prohibidos. Con eso lo digo todo.
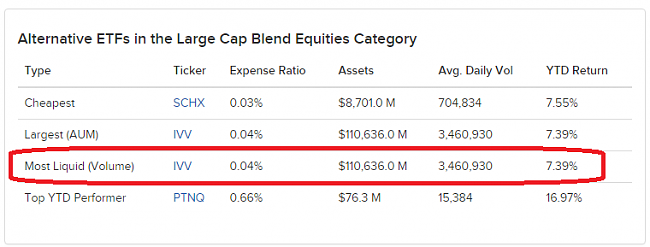
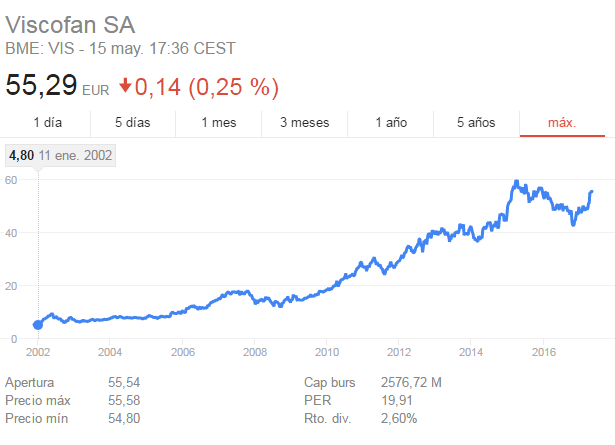
Los ETFs que utilizo tienen más de 1000 millones en activos, algunos hasta 150.000 millones de dólares, con ello vas a tener los menores Spreads, y van a ser muy líquidos. El único problema hasta ahora eran las elevadas comisiones que te cobraban los brokers, no podía ser que si hicieras 50 operaciones al año se quedaran 1500 euros en comisiones... ahora igual con DE GIRO son 200 euros... es una diferencia importante.
Un Saludo.


 13Likes
13Likes LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks






 Citar
Citar









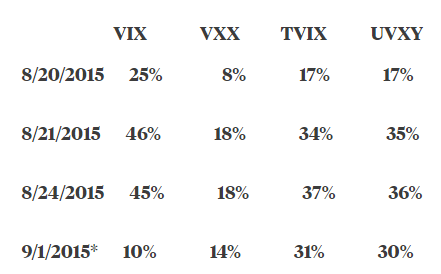








Marcadores